목차

1. 근의 공식이란?
중학교에서 공부를 했던 사람이라면 한 번씩은 꼭 들어봤을 법한 근의 공식, 알고 계신가요? 근의 공식은 이차방정식의 근를 구하고 싶을 때 이차방정식의 각 항의 계수를 이용하여 근을 구하는 공식을 말합니다.

위의 식은 우리가 잘 알고 있는 이차방정식의 근의 공식이죠. 이때 혹시나 이해하기 힘든 분들을 위해 어떤 방식으로 적용이 되는 것인지 아래에 예시를 적어보겠습니다.

자 그렇다면 이번 포스트에서는 이차방정식의 근의 공식이 왜 저런 복잡한 형태를 가지고 있는지 이차방정식을 해결하기 위해 어떤 방식을 가지고 해결하는지 자세히 알아보는 시간을 가져보도록 하겠습니다.
2. 근의 공식을 이해하기 위해 알아야 할 것들
이차방정식의 근의 공식을 제대로 이해하기 위해서는 알고 있어야 하는 중학교 수준의 수학 개념이 있습니다.
2.1. 제곱근
거듭제곱은 알고 계실거라 생각합니다.

같은 수를 2번 곱하는 것을 거듭제곱이라고 하죠. 그럼 거꾸로 생각해봅시다.

어떤 수를 제곱했을 때 16이 되게 하는 x는 무엇이 있을까요? 4를 생각하셨다고요? 물론 그것도 틀린 건 아닙니다. 하지만 -4도 제곱하면 16이 되죠? 이 부분을 조심해야 합니다.
결론적으로 제곱근이란 제곱하면 a가 되는 수를 a의 제곱근이라고 합니다. 식으로 다시 쓰면
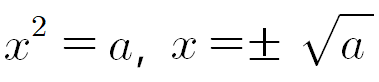
이렇게 정리할 수 있겠네요.
2.2. 완전제곱식
완전제곱식이란 다항식의 제곱으로 된 식 또는 다항식의 제곱에 상수를 곱한 식을 말합니다.

위와 같은 식들을 완전제곱식이라고 합니다. 그렇다면 이번에도 거꾸로 생각해봅시다.

위 식을 완전제곱식으로 바꾸려면 어떻게 해야할까요?
먼저 x²의 계수가 1이므로 완전제곱식의 형태는 아래처럼 될 것입니다.

숫자를 모르니 상수 a, b로 나타내었습니다. 위 식을 전개해보면

가 됩니다. 그렇다면 이 식이 주어진 식과 같아야겠죠?

정리하면 위 등식이 성립해야겠습니다. 즉, x의 계수와 상수항끼리 같아야 함을 의미하죠.

이렇게 정리할 수 있습니다. a는 3이 되고 b는 -9가 되겠네요.

완전제곱식으로 바꾼 결과입니다. 여러분은 이 예시에서 어떠한 메커니즘을 찾으셨나요?
제가 노란색으로 강조한 단계에서 이해해야할 중요한 점은
이차식을 완전제곱식으로 바꾸기 위해서는 x의 계수의 절반을 제곱한 수를 더하고 뺀다는 것입니다.
주어진 예시에서 x의 계수는 6이었습니다. 6으로 절반으로 나누면 3이 되죠. 3을 제곱하면 9가 됩니다.
그래서 원래 식에 9를 더하고 빼주면 식을 이렇게 바꿀 수 있겠죠?

이런 과정을 거쳐 완전제곱식을 만든다는 것을 이해했다면 근의 공식 증명의 준비는 끝났습니다.
3. 근의 공식 증명
이제 본격적으로 증명하겠습니다. 이차방정식의 근을 구하는 근의 공식이 어떻게 나오는지 지켜보세요.

이차방정식이 있습니다. 양변을 a로 나누겠습니다. (이차방정식이니 당연히 a는 0이 아니겠죠?)

자 그럼 이제 제곱근에서 배운 원리를 적용시키기 위해 위의 식을 완전제곱식으로 바꾸어 보겠습니다.
x의 계수의 절반을 제곱한 값을 더하고 빼는 거 잊지 않으셨죠?

완전제곱식으로 보기 좋게 변형해볼게요.


이제 제곱근의 정의를 가지고 양변에 루트를 씌워보겠습니다.

양변에 -b/2a를 더하면

우리가 알고 있는 근의 공식을 증명했습니다.
4. 근의 공식 정리
어떠신가요? 생각보다 그렇게 어렵지 않죠? 근의 공식은 제곱근와 완전제곱식이라는 개념을 제대로 이해하고 활용한다면 이차방정식의 해를 간단하게 구할 수 있습니다. 단순히 근의 공식을 암기하는 것이 아니라 구조를 이해하고 증명 과정을 찬찬히 살펴본다면 수학이 여러분에게 그렇게 어려운 과목은 아니게 느껴질 것이라 자부합니다! 이번 포스트는 여기서 마무리하고 더 많은 수학 소식과 여러 증명, 활용 등을 익히고 싶다면 왓수의 매쓰토리를 구독해주시고 많이 들어와주세요 감사합니다 :)
'중학수학 증명' 카테고리의 다른 글
| 피타고라스 정리를 증명하는 5가지 방법 (0) | 2023.06.15 |
|---|